Deep Neural Networks with PyTorch

Saturday. August 29, 2020 - 12 mins

Cost Function

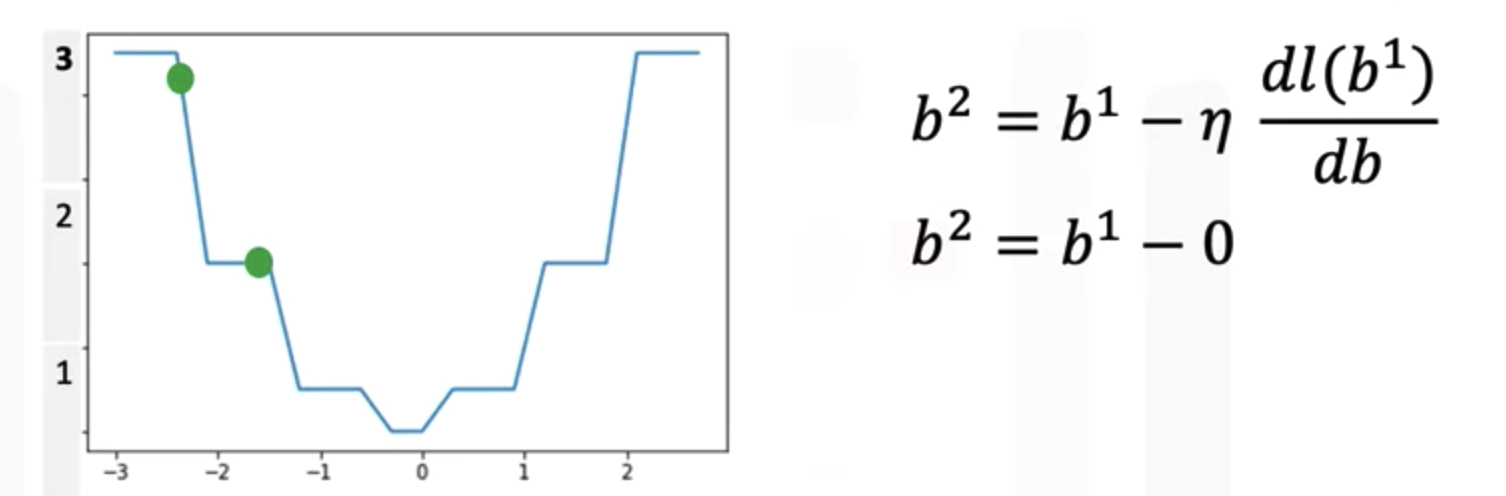
What’s the problem with using the cost function generated using the threshold function?

A: It is flat in some regions, which stucks the gradient decent for updating parameters. To avoid this issues in logistic regression, we use cross entropy loss function (negatitive maximum likelihood function) as the loss function instead of MSE.

Threshold Function

Vanishing gradients

What is the problem with the tanh and sigmoid activation function?

A: The value of the gradient of the tanh and sigmoid activation function becomes very small for the deeper hidden layers. It is because their derivates is near zero in many region. To avoid this issue, we often see the Relu activation function been used in this situation.

Problems with not initializing weights

What happen if we intialize weights with the same value?

A: It causes our neural net works doing horrible jobs on the predicion. Because the finial weight for each neuron is the same. Pytorch takes care of the weights intialization step from us by sampling from an uniformly distribution and the width of the distribution is given by the number of neurons.
How to fix the problem with vanishing gradients due to a large number of neuron?

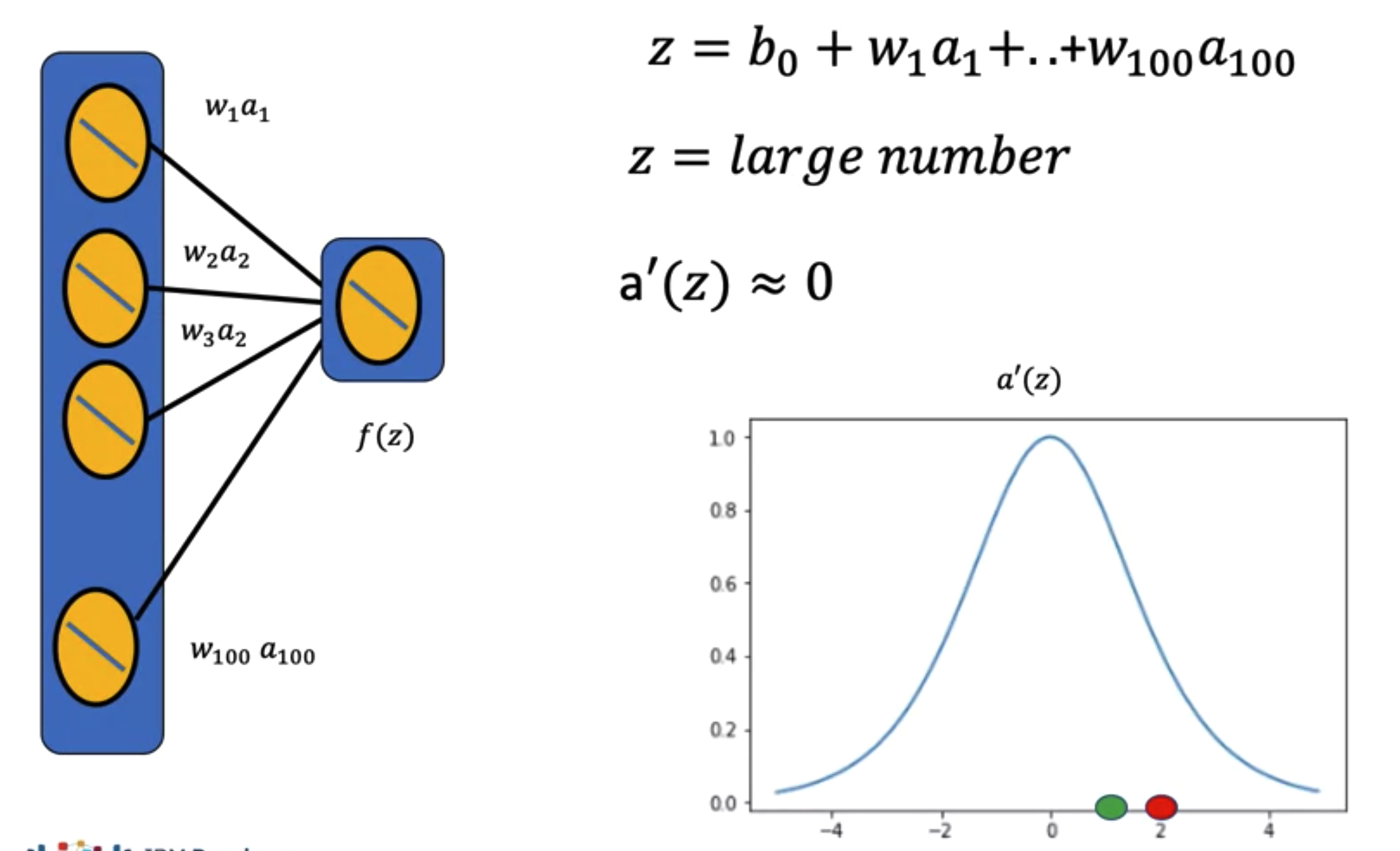
A: We could scale the width of the distribution by the inverse of the number of neurons. So if we have 2 neurons, we scaled the width of the distribution by one half. We can obtian any value from -1/2 to 1/2.
Different initilization method in Pytorch.
- Default Method:
\[[-\frac{1}{\sqrt L_{in}},\frac{1}{\sqrt L_{in}}], where\ L_{in}\ is \ the \ number\ of\ input\ neron\]
- Xavier Method: It is used in conjuction of tanh activation.
```
  linear = nn.Linear(input_size,output_size)
  torch.nn.init.xavier_uniform_(linear.weight)
```
\[[-\frac{6}{\sqrt L_{in} + \sqrt L_{out}},\frac{6}{\sqrt L_{in} + \sqrt L_{out}}], \\ L_{in}\ is \ the \ number\ of\ input\ neron;\\ L_{out}\ is \ the \ number\ of\ neron\ in\ next\ layer\]
- He Method: It is used in conjuction of Relu activation function.
```
  linear = nn.Linear(input_size,output_size)
  torch.nn.init.kaiming_uniform_(linear.weight,nonlinearity='relu')
```

Gradient descent with Momenturm

Terminology

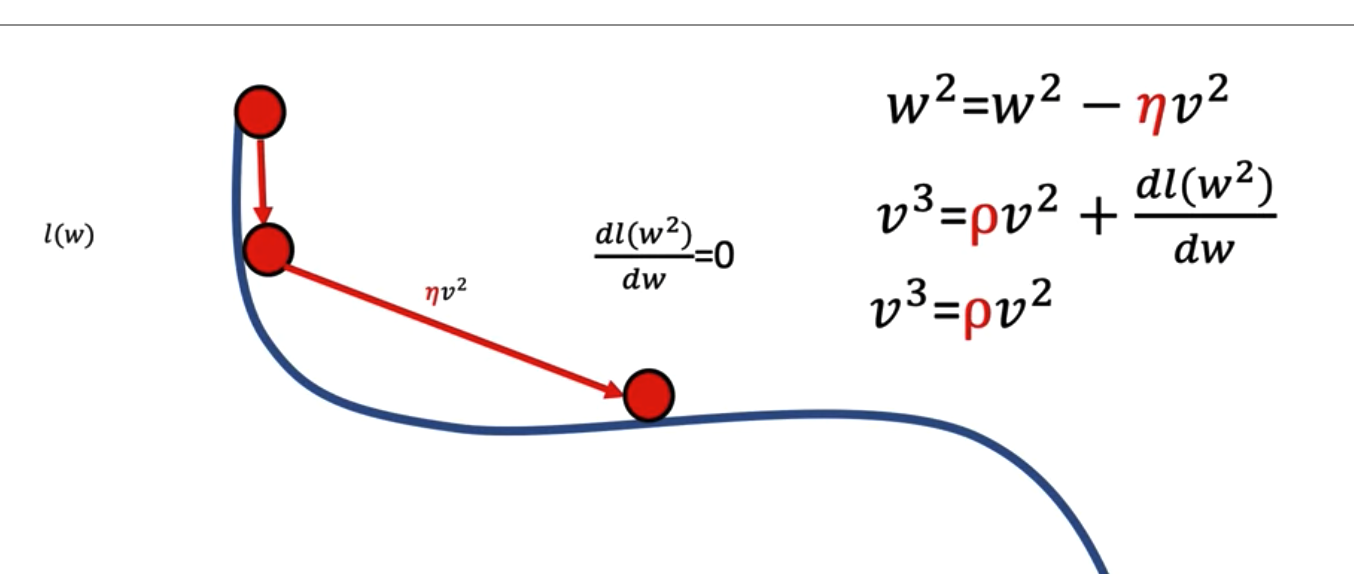
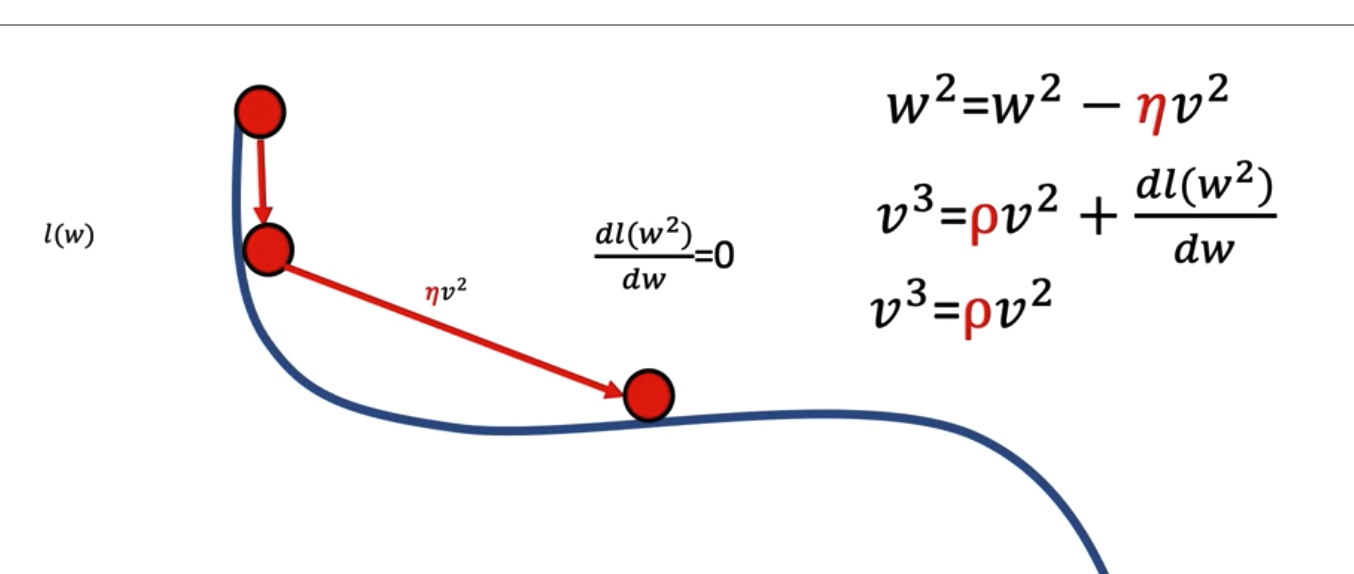
Saddle points: Flat points in a surface, which prevent updating the weight.
Momentum: A hyperparameter we use to scale previous velocity on updating current weight. This allow us to achieve an non-zero velocity on current iteration even when the graph for the loss is flat. It also help us to overcome local minimum problem. If the value of the momenturm is small, we will stack in the local minimum. If the value of the momentum is large, we might overshoot the global mimimum.

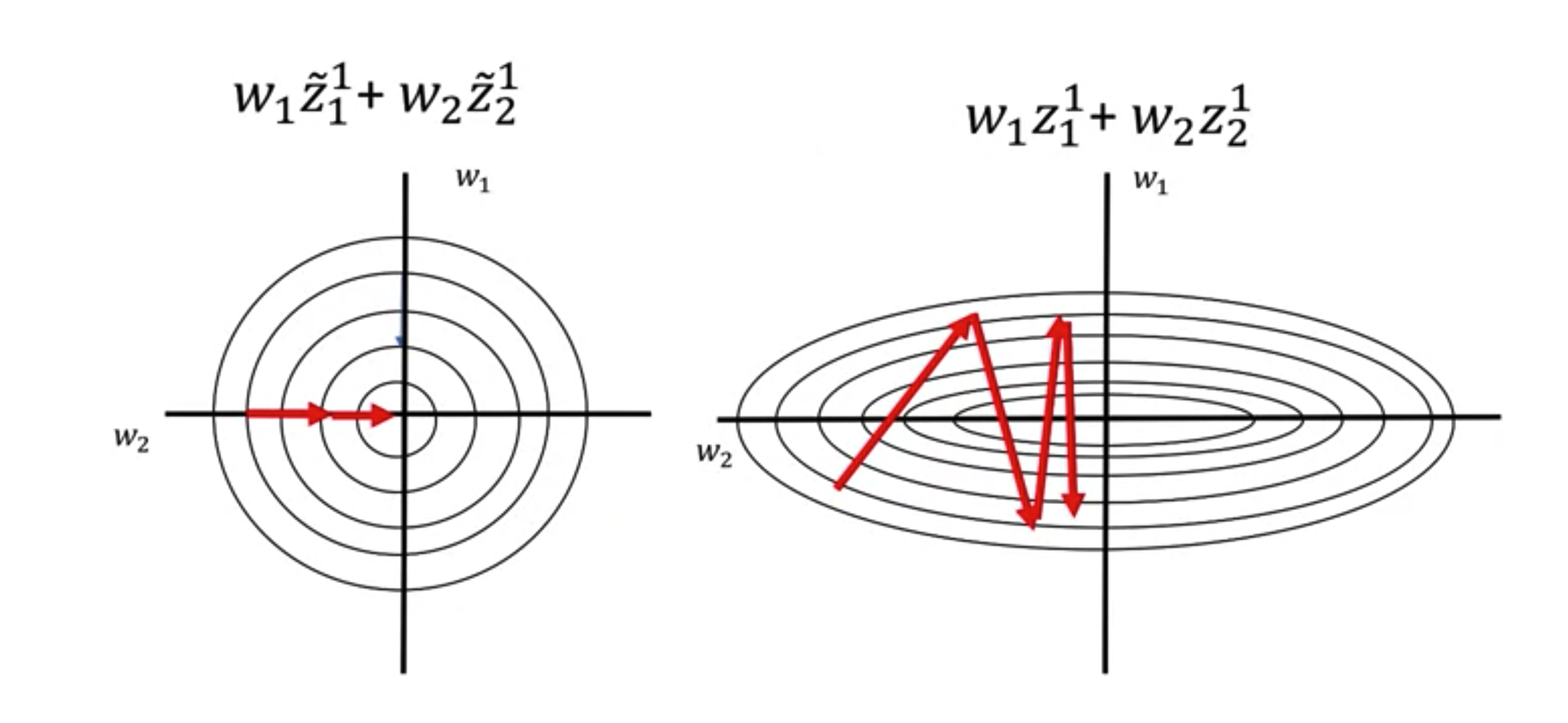
Batch Normalization

The batch normalization happens for each neuron before we pass it to activation function.

Training Part

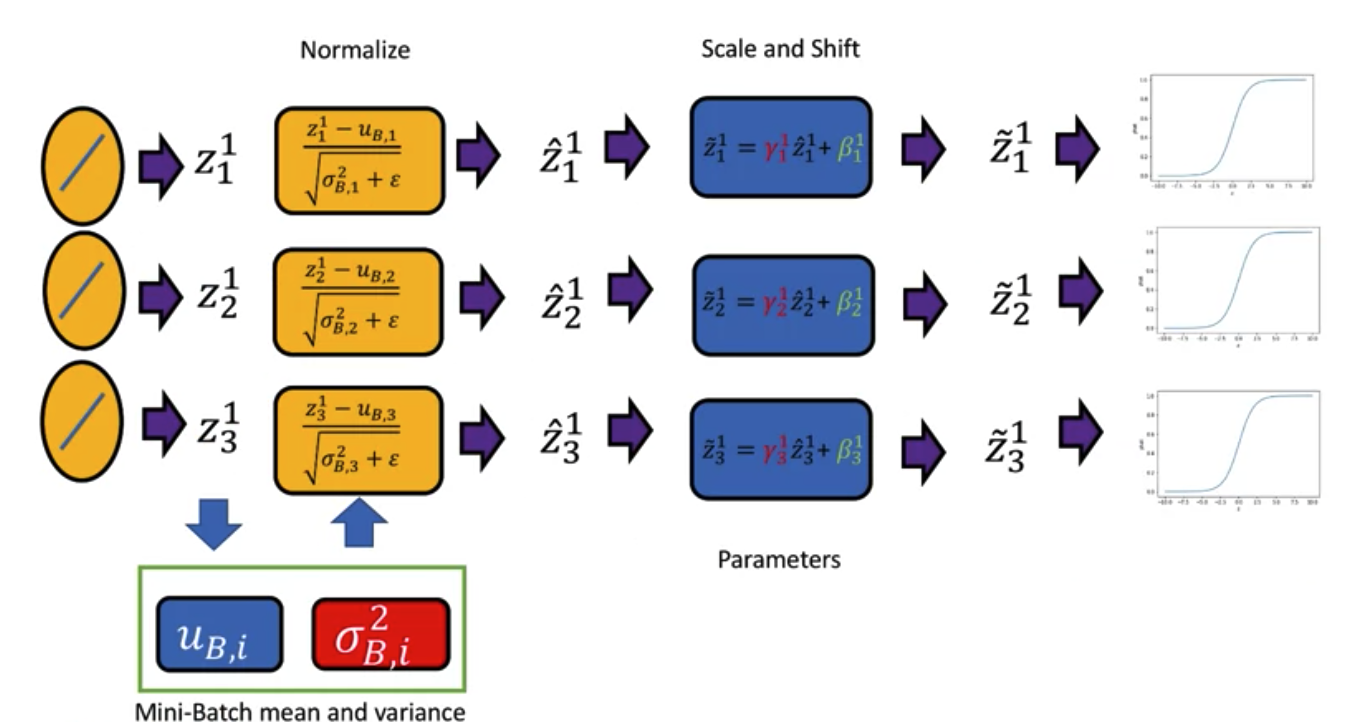
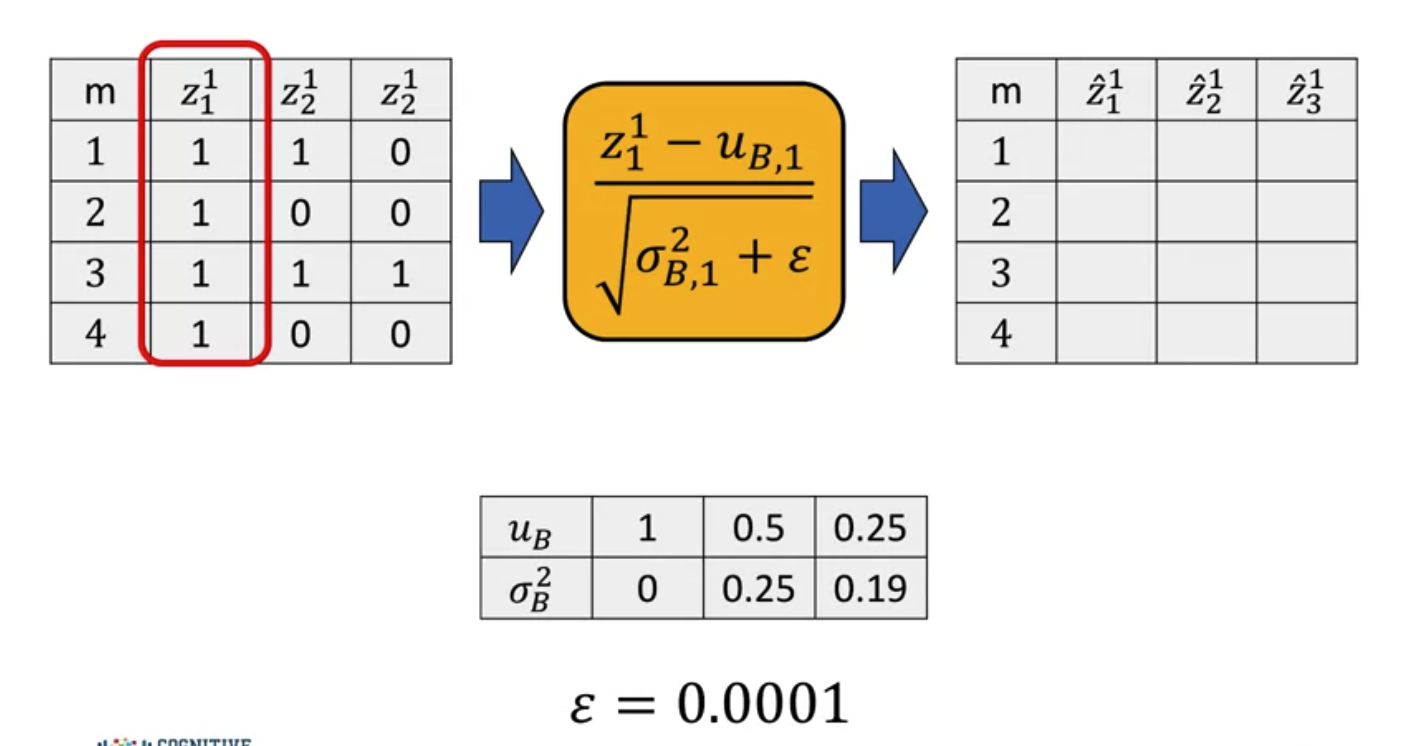
Prediction Part:

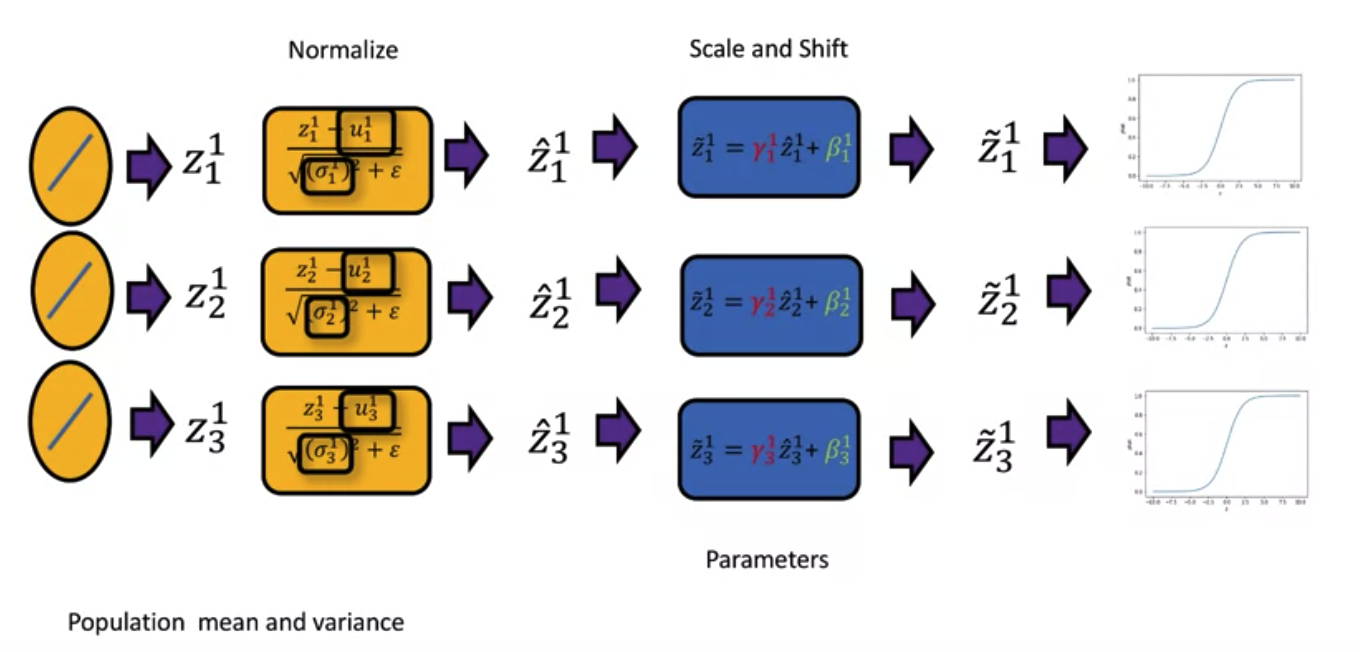
The mean and variance fo each neuron is estimated by the entire population.

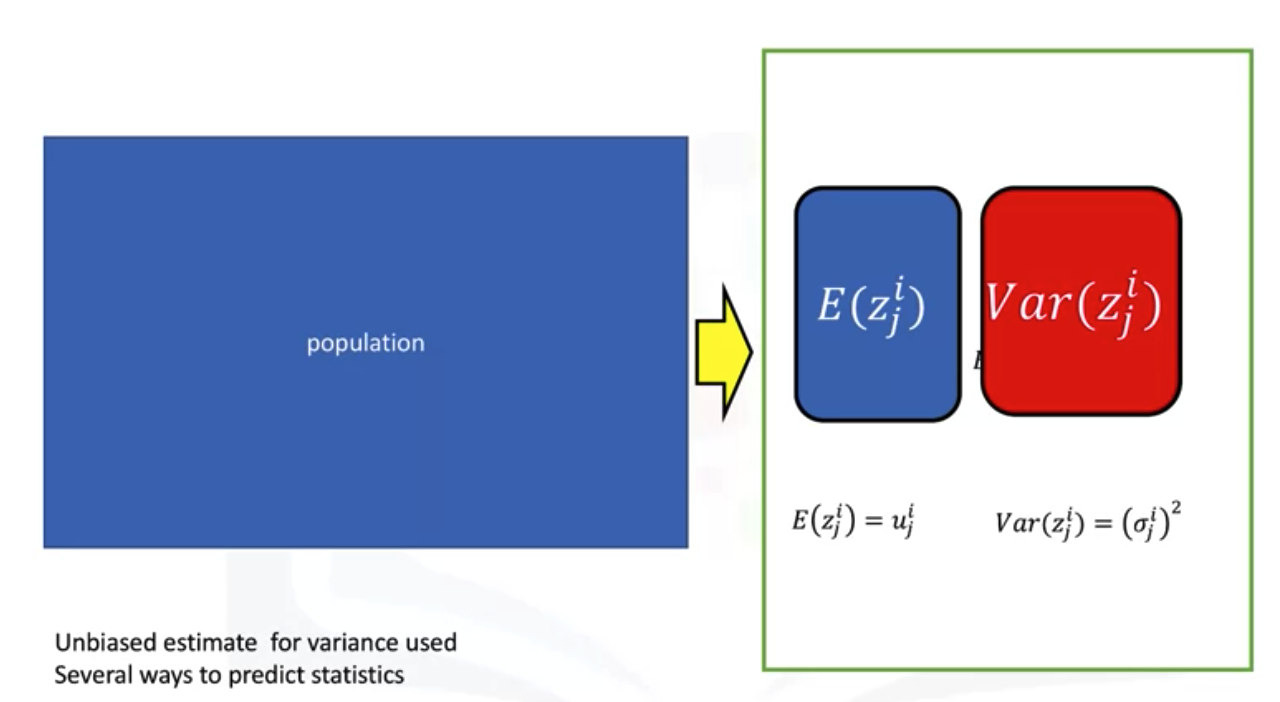
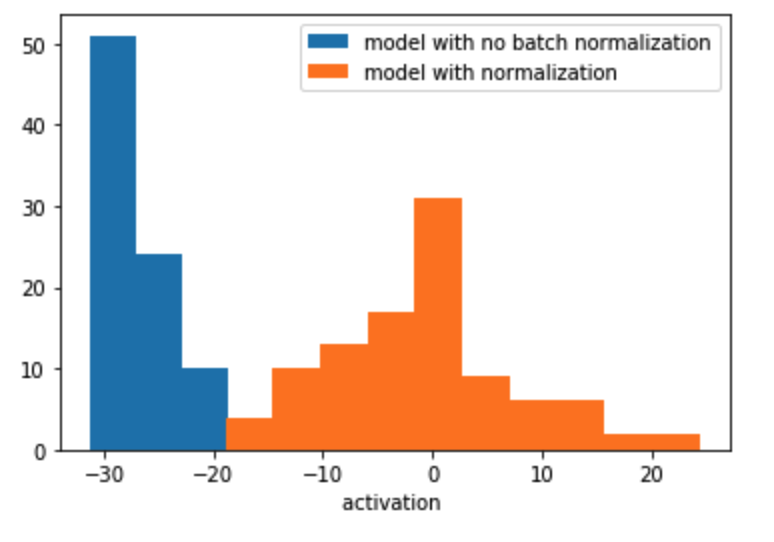
Why Batch normalization works?

It take short time to converge as:

it reduce internal covariate shift
remove dropout
increasing learning rate
bias is not necessary

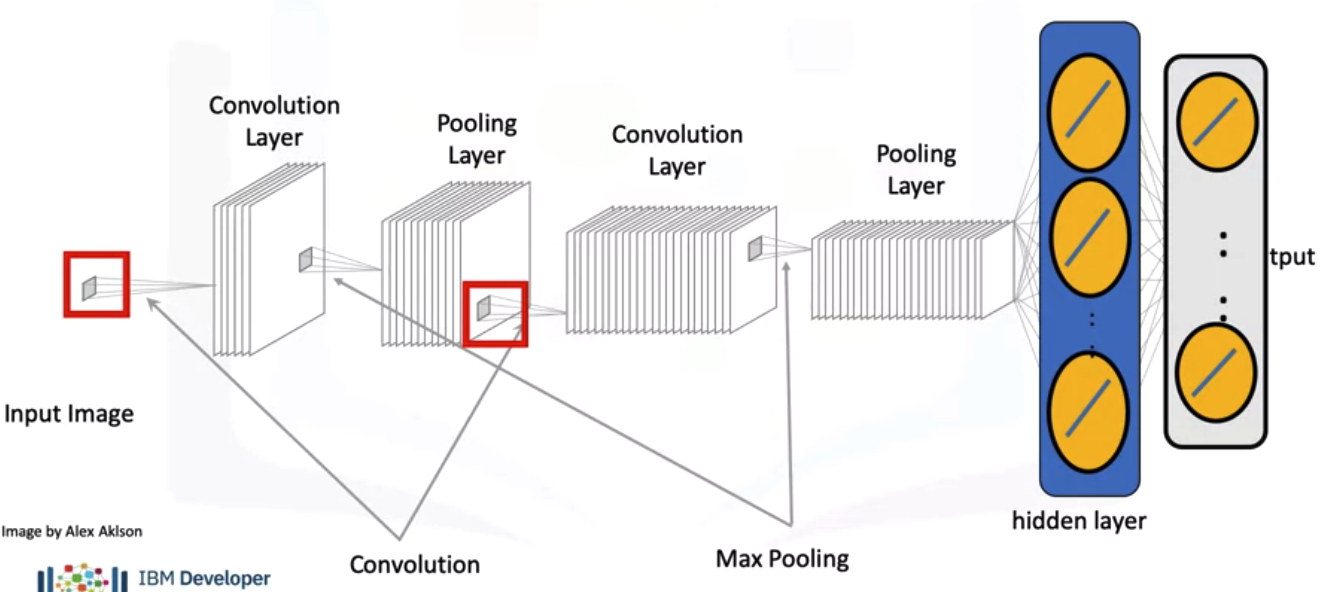
Convolution

Convolution is a linear operation similar to a linear equation, dot product, or matrix multiplication. Convolution has several advantages for analyzing images. As discussed in the video, convolution preserves the relationship between elements, and it requires fewer parameters than other methods.

You can see the relationship between the different methods that you learned:

In convolution, the parameter w is called a kernel. You can perform convolution on images where you let the variable image denote the variable X and w denote the parameter.

Illustration

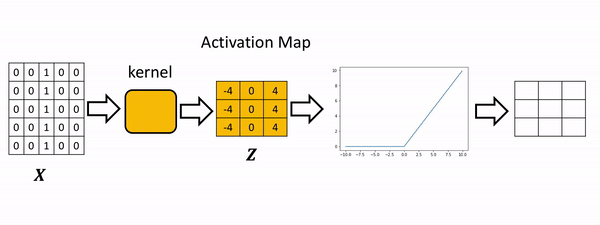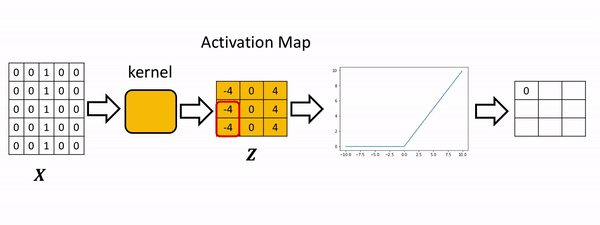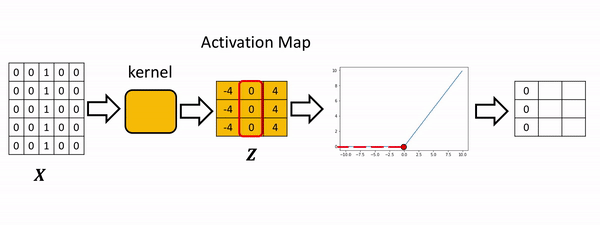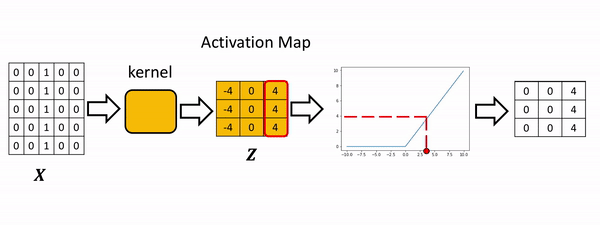
Terminology

Kernel: A weight matrix to do dot multiplication on a part of input matrix and then move a stride forward.

Stride: The parameter stride changes the number of shifts the kernel moves per iteration. As a result, the output size also changes and is given by the following formula.

\[M_{new}=\dfrac{M-K}{stride}+1\]

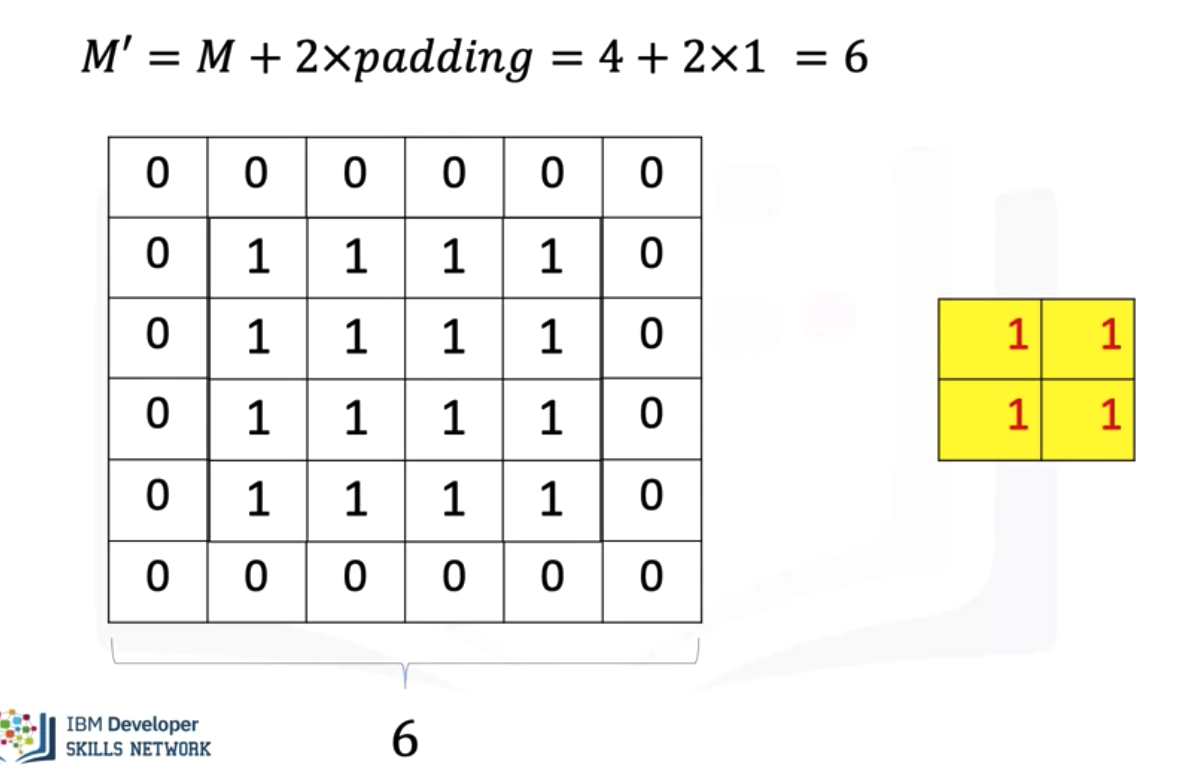
Zero Padding: As you apply successive convolutions, the image will shrink. You can apply zero padding to keep the image at a reasonable size, which also holds information at the borders. You can add rows and columns of zeros around the image. This is called padding. In the constructor Conv2d you specify the number of rows or columns of zeros that you want to add with the parameter padding. For a square image, you merely pad an extra column of zeros to the first column and the last column. Repeat the process for the rows. As a result, for a square image, the width and height is the original size plus 2 x the number of padding elements specified. You can then determine the size of the output after subsequent operations accordingly as shown in the following equation where you determine the size of an image after padding and then applying a convolutions kernel of size K.

\[M'=M+2 \times padding \\ M_{new}=M'-K+1\]

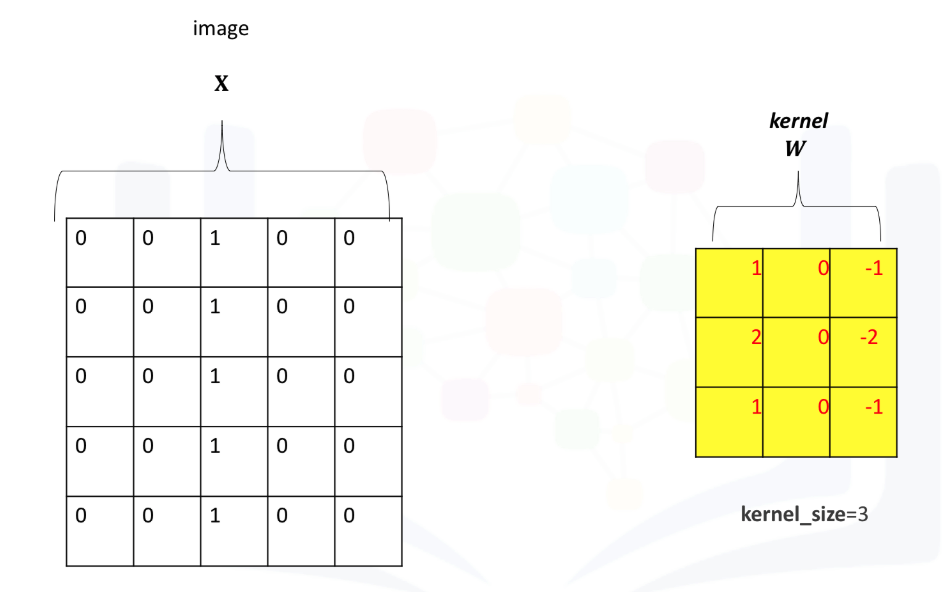
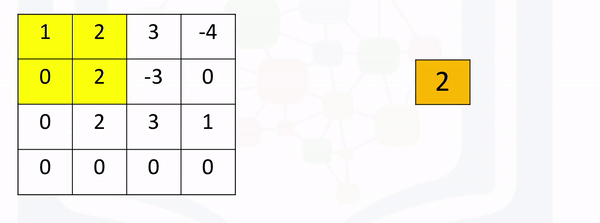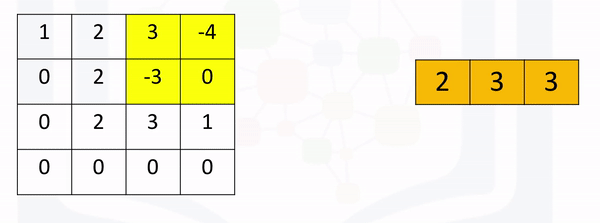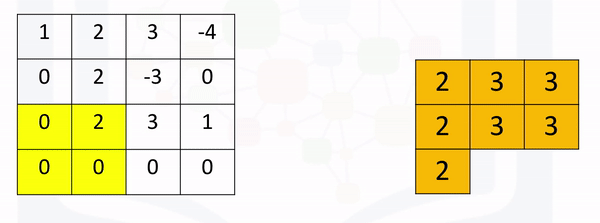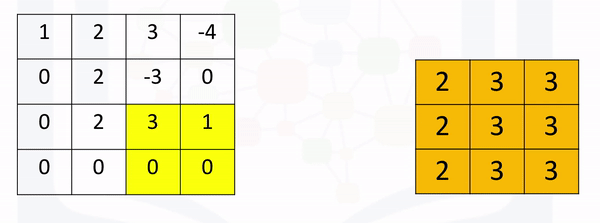
Max Pooling: Max pooling simply takes the maximum value in each region. Consider the following image. For the first region, max pooling simply takes the largest element in a yellow region.

Multiple Channels

Multiple Output Channels:

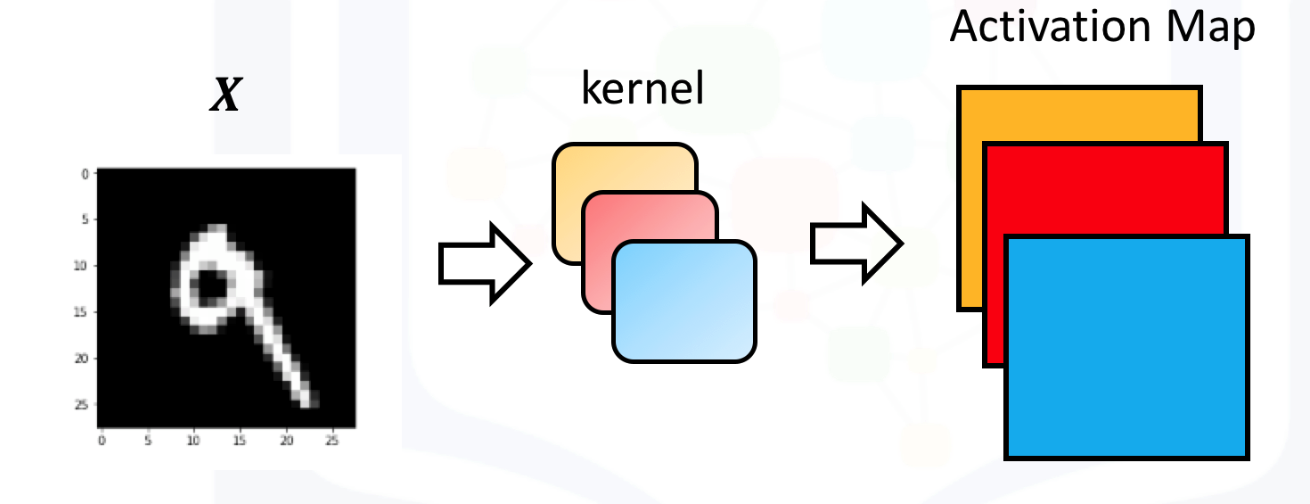
In Pytorch, you can a Conv2d object with multiple outputs. For each channels, a kernel is created, and each channels performs convolution independently. As a result, the number of ouputs is equal to the number of channels. This is demonstrated in the following figure. The number of 9 is convolved with thress kernels, each of a different color. There are three different activation maps represented by the different colors.

Multiple Input Channels:

For multiple inputs, you can create multiple kernels. Each kernel performs a convolution on its associated input channel. The resulting output is added together as shown:

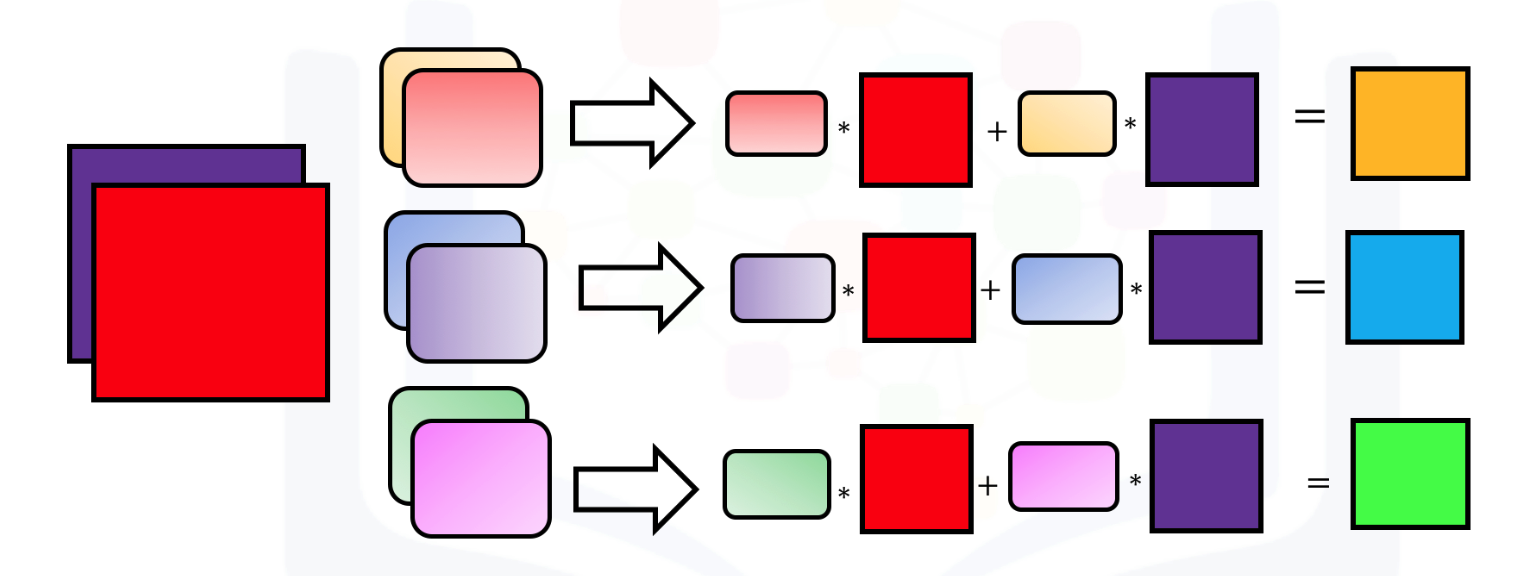
Mutiple output and input Channels:

When using multiple inputs and outputs, a kernel is created for each input, and process is repeated for each output. This process is summarized in the following figure:

There are 3 output channels and 2 input channels. For each channels, the input in red and purple is convolved with an individual kernel that is colored differently. As a results, there are three outputs.

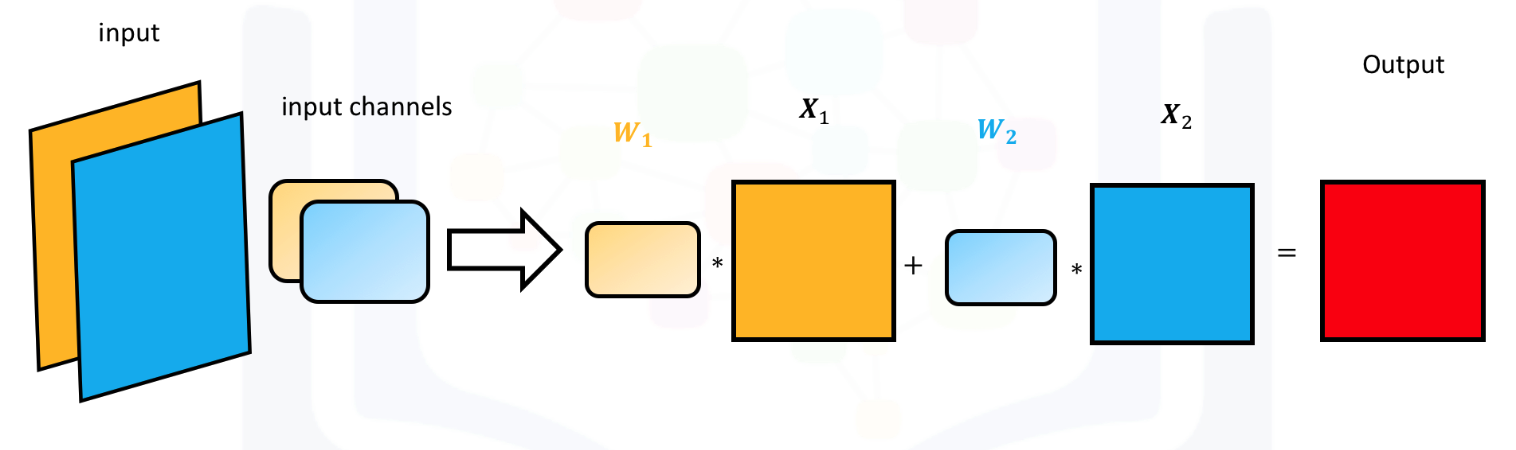
Convolution Neural Network

Batch Normalization before Max pooling

Like a fully connected network, we create a BatchNorm2d object, but we apply it to the 2D convolution object. First, we create objects Conv2dobject; we require the number of output channels, specified by the variable OUT.

self.cnn1 = nn.Conv2d(in_channels=1, out_channels=OUT, kernel_size=5, padding=2)
# We then create a Batch Norm  object for 2D convolution as follows:
self.conv1_bn = nn.BatchNorm2d(OUT)
# The parameter out is the number of channels in the output. 
# We can then apply batch norm  after  the convolution operation :
x = self.cnn1(x)
x=self.conv1_bn(x)

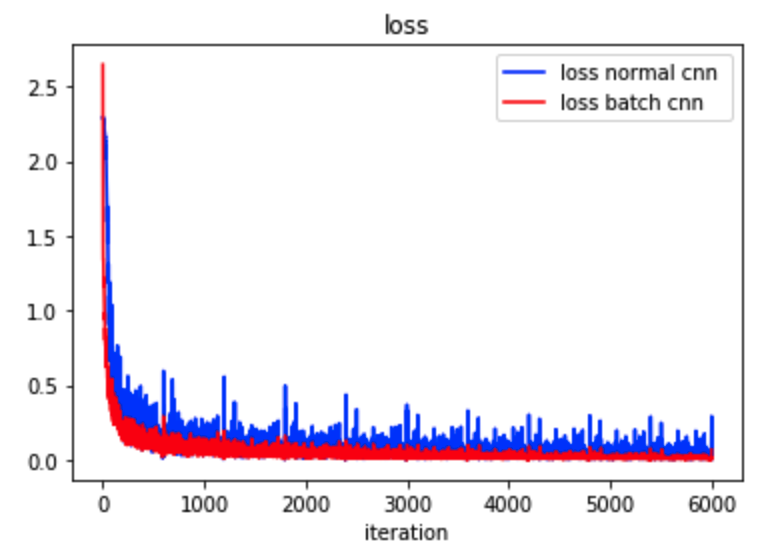
Compare convolution neural network with batch normalization and without on MINIST image dataset.

class CNN(nn.Module):
    
    # Contructor
    def __init__(self, out_1=16, out_2=32):
        super(CNN, self).__init__()
        self.cnn1 = nn.Conv2d(in_channels=1, out_channels=out_1, kernel_size=5, padding=2)
        self.maxpool1=nn.MaxPool2d(kernel_size=2)

        self.cnn2 = nn.Conv2d(in_channels=out_1, out_channels=out_2, kernel_size=5, stride=1, padding=2)
        self.maxpool2=nn.MaxPool2d(kernel_size=2)
        self.fc1 = nn.Linear(out_2 * 4 * 4, 10)
    

    # Prediction
    def forward(self, x):
        x = self.cnn1(x)
        x = torch.relu(x)
        x = self.maxpool1(x)
        x = self.cnn2(x)
        x = torch.relu(x)
        x = self.maxpool2(x)
        x = x.view(x.size(0), -1)
        x = self.fc1(x)
        return x

class CNN_batch(nn.Module):
    
    # Contructor
    def __init__(self, out_1=16, out_2=32,number_of_classes=10):
        super(CNN_batch, self).__init__()
        self.cnn1 = nn.Conv2d(in_channels=1, out_channels=out_1, kernel_size=5, padding=2)
        self.conv1_bn = nn.BatchNorm2d(out_1)

        self.maxpool1=nn.MaxPool2d(kernel_size=2)
        
        self.cnn2 = nn.Conv2d(in_channels=out_1, out_channels=out_2, kernel_size=5, stride=1, padding=2)
        self.conv2_bn = nn.BatchNorm2d(out_2)

        self.maxpool2=nn.MaxPool2d(kernel_size=2)
        self.fc1 = nn.Linear(out_2 * 4 * 4, number_of_classes)
        self.bn_fc1 = nn.BatchNorm1d(10)
    
    # Prediction
    def forward(self, x):
        x = self.cnn1(x)
        x=self.conv1_bn(x)
        x = torch.relu(x)
        x = self.maxpool1(x)
        x = self.cnn2(x)
        x=self.conv2_bn(x)
        x = torch.relu(x)
        x = self.maxpool2(x)
        x = x.view(x.size(0), -1)
        x = self.fc1(x)
        x=self.bn_fc1(x)
        return x

Pretrain Model on Pytorch:

You can load a pre-train model as followiyng and only train you model to update the last layer:

model = models.densenet121(pretrained=True)
for param in model.parameters:
	param.requires_grad = False

model.fc = nn.linear(512,7) # replace the last layer by your own fully connected layer 

optimizer = torch.optim.SGD([
	p for p in model.parameters() if x.requires_grad
	],lr = learning_rate)

Jingxin Fu, Ph.D.

Research Fellow interested in data mining on cancer genomics